VoteBox: a tamper-evident, verifiable electronic voting system

Daniel Sandler      Kyle Derr       Dan S. Wallach
Rice University
{dsandler,derrley,dwallach}@cs.rice.edu

1  Introduction

Electronic voting is at a crossroads. Having been aggressively deployed across the United States as a response to flawed paper and punch-card voting in the 2000 U.S. national election, digital-recording electronic (DRE) voting systems are themselves now seen as flawed and unreliable. They have been observed in practice to produce anomalies that may never be adequately explained—undervotes, ambiguous audit logs, choices “flipping” before the voter's eyes. Recent independent security reviews commissioned by the states of California and Ohio have revealed that every DRE voting system in widespread use has severe deficiencies in design and implementation, exposing them to a wide variety of vulnerabilities; these systems were never engineered to be secure. As a result, many states are now decertifying or restricting the use of DRE systems.

Consequently, DREs are steadily being replaced with systems employing optical-scan paper ballots. Op-scan systems still have a variety of problems, ranging from accessibility issues to security flaws in the tabulation systems, but at least the paper ballots remain as evidence of the voter's original intent. This allows voters some confidence that their votes can be counted (or at least recounted) properly. However, as with DRE systems, if errors or tampering occur anywhere in this process, there is no way for voters to independently verify that their ballots were properly tabulated.

Regardless, voters subjectively prefer DRE voting systems [15]. DREs give continuous feedback, support many assistive devices, permit arbitrary ballot designs, and so on. Furthermore, unlike vote-by-mail or Internet voting, DREs, used in traditional voting precincts, provide privacy, protecting voters from bribery or coercion. We would ideally like to offer voters a DRE-style voting system with additional security properties, including:

1. Minimized software stack
2. Resistance to data loss in case of failure or tampering
3. Tamper-evidence: a record of election day events that can be believably audited
4. End-to-end verifiability: votes are cast as intended and counted as cast

The subject of this paper is the VoteBox, a complete electronic voting system that offers these essential properties as well as a number of other advantages over existing designs. Its user interface is built from pre-rendered graphics, reducing runtime code size as well as allowing the voter's exact voting experience to be examined well before the election. VoteBoxes are networked in a precinct and their secure logs are intertwined and replicated, providing robustness and auditability in case of failure, misconfiguration, or tampering. While all of these techniques have been introduced before, the novelty of this work lies in our integration of these parts to achieve our architectural security goals.

Notably, we use a technique adapted from Benaloh's work on voter-initiated auditing [4] to gain end-to-end verifiability. Our scheme, which we term immediate ballot challenge, allows auditors to compel any active voting machine to produce proof that it has correctly captured the voter's intent. With immediate challenges, every single ballot may potentially serve as an election-day test of a VoteBox's correctness. We believe that the VoteBox architecture is robust to the kinds of failures that commonly occur in elections and is sufficiently auditable to be trusted with the vote.

In the next section we will present background on the electronic voting problem and the techniques brought to bear on it in our work. We expand on our design goals and describe our VoteBox architecture in Section 3, and share details of our implementation in Section 4. The paper concludes with Section 5.

2  Background

2.1  Difficulties with electronic voting

While there have been numerous reports of irregularities with DRE voting systems in the years since their introduction, the most prominent and indisputable problem concerned the ES&S iVotronic DRE systems used by Sarasota County, Florida, in the November 2006 general election. In the race for an open seat in the U.S. Congress, the margin of victory was only 369 votes, yet over 18,000 votes were officially recorded as “undervotes” (i.e., cast with no selection in this particular race). In other words, 14.9% of the votes cast on Sarasota's DREs for Congress were recorded as being blank, which contrasts with undervote rates of 1–4% in other important national and statewide races. While a variety of analyses were conducted of the machines and their source code [18, 19, 51], the official loser of the election continued to challenge the results until a Congressional investigation failed to identify the source of the problem [3]. Whether the ultimate cause was mechanical failure of the voting systems or poor human factors of the ballot design, there is no question that these machines failed to accurately capture the will of Sarasota's voters [2, 14, 20, 25, 34, 36, 37, 50].

While both security flaws and software bugs have received significant attention, a related issue has also appeared numerous times in real elections using DREs: operational errors and mistakes. In a 2006 primary election in Webb County, Texas—the county's first use of ES&S iVotronic DRE systems—a number of anomalies were discovered when, as in Sarasota, a close election led to legal challenges to the outcome [46]. Test votes were accidentally counted in the final vote tallies, and some machines were found to have been “cleared” on election day, possibly erasing votes. More recently, in the January, 2008 Republican presidential primary in South Carolina, several ES&S iVotronic systems were incorrectly configured subsequent to pre-election testing, resulting in those machines being inoperable during the actual election. “Emergency” paper ballots ran out in many precincts and some voters were told to come back later [11].

All of these real-world experiences, in conjunction with recent highly critical academic studies, have prompted a strong backlash against DRE voting systems or even against the use of computers in any capacity in an election. However, computers are clearly beneficial.

Clearly, computers cannot be trusted to be free of tampering or bugs, nor can poll workers and election officials be guaranteed to always operate special-purpose computerized voting systems as they were intended to be used. Our challenge, then, is to reap the benefits that computers can offer to the voting process without being a prisoner to their costs.

2.2  Toward software independence

Recently, the notion of software independence has been put forth by Rivest and other researchers seeking a way out of this morass:

A voting system is software-independent if an undetected change or error in its software cannot cause an undetectable change or error in an election outcome.  [41]

Such a system produces results that are verifiably correct or incorrect irrespective of the system's implementation details; any software error, whether malicious or benign, cannot yield an erroneous output masquerading as a legitimate cast ballot.

Conventionally, the only way to achieve true software independence is to allow the voter to directly inspect, and therefore confirm to be correct, the actual cast vote record. Since we cannot give voters the ability to read bits off a flash memory card, nor can we expect them to mentally perform cryptographic computations, we are limited in practice to paper-based vote records, which can be directly inspected.

Optical-scan voting systems, in which the voter marks a piece of paper that is both read immediately by an electronic reader/tabulator and reserved in case of a manual audit, achieve this goal at the cost of sacrificing some of the accessibility and feedback afforded by DREs. The voter-verifiable paper audit trail (VVPAT) allows a DRE to create a paper record for the voter's inspection and for use in an audit, but it has its own problems. Adding printers to every voting station dramatically increases the mechanical complexity, maintenance burden, and failure rate of those machines. A report on election problems in the 2006 primary in Cuyahoga County, Ohio found that 9.6% of VVPAT records were destroyed, blank, or “compromised in some way” [23,p. 93].

Even if the voter's intent survives the printing process, the rolls of thermal paper used by many current VVPAT printers are difficult to audit by hand quickly and accurately [22]. It is also unclear whether voters, having already interacted with the DRE and confirmed their choices there, will diligently validate an additional paper record. (In the same Cuyahoga primary election, a different report found that voters in fact did not know they were supposed to open a panel and examine the printed tape underneath [1,p. 50].)

2.2.1  Reducing the trusted computing base

While the goal of complete software independence is daunting, the state of the art in voting research approaches it by drawing a line around the set of functions that are essential to the correctness of the vote and aggressively evicting implementation from that set. If assurance can come from reviewing and auditing voting software, then it should be easier to review and ultimately gain confidence in a smaller software stack.

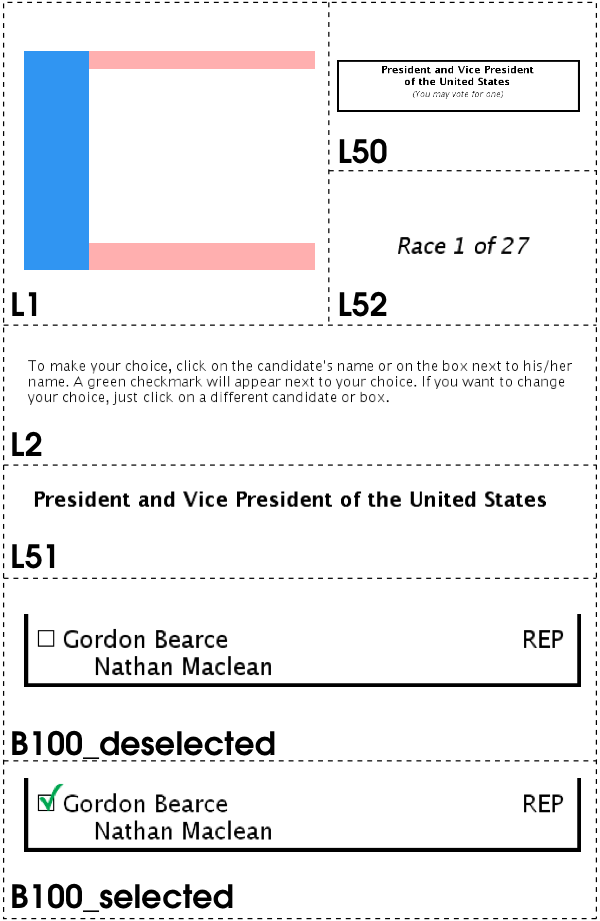
Pre-rendered user interface (PRUI) is an approach to reducing the amount of voting software that must be reviewed and trusted [53]. Exemplified by Pvote [52], a PRUI system consists of a ballot definition and a software system to present that ballot. The ballot definition comprises a state machine and a set of static bitmap images corresponding to those states; it represents what the voter will see and interact with. The software used in the voting machine acts as a virtual machine for this ballot “program.” It transitions between states and sends bitmaps to the display device based on the voter's input (e.g., touchscreen or keypad). The voting VM is no longer responsible for text rendering or layout of user interface elements; these tasks are accomplished long in advance of election day when the ballot is defined by election officials.

A ballot definition of this sort can be audited for correctness independently of the voting machine software or the ballot preparation software. Even auditors without knowledge of a programming language can follow the state transitions and proofread the ballot text (already rendered into pixels). The voting machine VM should still be examined by software experts, but this code—critical to capturing the user's intent—is reduced in size and therefore easier to audit. Pvote comprises just 460 lines of Python code, which (even including the Python interpreter and graphics libraries) compares favorably against current DREs: the AccuVote TS involves over 31,000 lines of C++ running atop Windows CE [52]. The system we describe in Section 3 applies the PRUI technique to reduce its own code footprint.

Sastry et al. [47] describe a system in which program modules that must be trusted are forced to be small and clearly compartmentalized by dedicating a separate computer to each. The modules operate on isolated CPUs and memory, and are connected with wires that may be observed directly; each module may therefore be analyzed and audited independently without concern that they may collude using side channels. Additionally, the modules may be powered off and on between voters to eliminate the possibility of state leaking from voter to voter. (Section 4.1 shows how we approximate this idea in software.)

2.2.2  The importance of audit logs

Even trustworthy software can be misused, and this problem occurs with unfortunate regularity in the context of electronic voting. We expect administrators to correctly deploy, operate, and maintain large installations of unfamiliar computer systems. DRE vendors offer training and assistance, but on election day there is typically very little time to wait for technical support while voters queue up.

In fact, the operational and procedural errors that can (and do) occur during elections is quite large. Machines unexpectedly lose power, paper records are misplaced, hardware clocks are set wrong, and test votes (see Section 2.2.3 below) are mingled with real ballots. Sufficient trauma to a DRE may result in the loss of its stored votes.

In the event of an audit or recount, comprehensive records of the events of election day are essential to establishing (or eroding) confidence in the results despite these kinds of election-day mishaps. Many DREs keep electronic audit logs, tracking election day events such as “the polls were opened” and “a ballot was cast,” that would ideally provide this sort of evidence to post facto auditing efforts. Unfortunately, current DREs entrust each machine with its own audit logs, making them no safer from failure or accidental erasure than the votes themselves. Similarly, the audit logs kept by current DREs offer no integrity safeguards and are entirely vulnerable to attack; any malicious party with access to the voting machine can trivially alter the log data to cover up any misdeeds.

The Auditorium [46] system confronts this problem by using techniques from distributed systems and secure logging to make audit logs into believable records. All voting machines in a polling place are connected in a private broadcast network; every election event that would conventionally be written to a private log is also “announced” to every voting machine on the network, each of which also logs the event. Each event is bound to its originator by a digital signature, and to earlier events from other machines via a hash chain. The aggressive replication protects against data loss and localized tampering; when combined with hash chains, the result is a hash mesh [48] encompassing every event in the polling place. An attacker (or an accident) must now successfully compromise every voting machine in the polling place in order to escape detection. (In Section 3 we describe how VoteBox uses and extends the Auditorium voting protocol.)

2.2.3  Logic and accuracy testing; parallel testing

Regrettably, the conventional means by which voting machines are deemed trustworthy is through testing. Long before election day, the certification process typically involves some amount of source code analysis and testing by “independent testing authorities,” but these processes have been demonstrably ineffective and insufficient. Logic and accuracy (L&A) testing is a common black-box testing technique practiced by elections officials, typically in advance of each election. L&A testing typically takes the form of a mock election: a number of votes are cast for different candidates, and the results are tabulated and compared against expected values. The goal is to increase confidence in the predictable, correct functioning of the voting systems on election day.

Complementary to L&A is parallel testing, performed on election day with a small subset of voting machines selected at random from the pool of “live” voting systems. The units under test are sequestered from the others; as with L&A testing, realistic votes are cast and tallied. By performing these tests on election day with machines that would otherwise have gone into service, parallel testing is assumed to provide a more accurate picture of the behavior of other voting machines at the same time.

The fundamental problem with these tests is that they are artificial: the conditions under which the test is performed are not identical to those of a real voter in a real election. It is reasonable to assume that a malicious piece of voting software may look for clues indicating a testing situation (wrong day; too few voters; evenly-spread voter choices) and behave correctly only in such cases. A software bug may of course have similar behavior, since faulty DREs may behave arbitrarily. We must also take care that a malicious poll worker cannot signal the testing condition to the voting machine using a covert channel such as a “secret knock” of user interface choices.

Given this capacity to “lay low” under test, the problem of fooling a voting machine into believing it is operating in a live vote-capture environment is paramount [26]. Because L&A testing commonly makes explicit use of a special code path, parallel testing is the most promising scenario. It presents its own unique hazard: if the test successfully simulates an election-day environment, any votes captured under test will be indistinguishable from legitimate ballots cast by real voters, so special care must be taken to keep these votes from being included in the final election tally.

2.3  Cryptography and e-voting

Many current DREs attempt to use encryption to protect the secrecy and integrity of critical election data; they universally fail to do so [6, 8, 24, 32]. Security researchers have proposed two broad classes of cryptographic techniques that go beyond simple encryption of votes (symmetric or public-key) to provide end-to-end guarantees to the voter. One line of research has focused on encrypting whole ballots and then running them through a series of mix-nets [9] that will re-encrypt and randomize ballots before they are eventually decrypted (see, e.g., [43, 35]). If at least one of the mixes is performed correctly, then the anonymity of votes is preserved. This approach has the benefit of tolerating ballots of arbitrary content, allowing its use with unconventional voting methods (e.g., preferential or Condorcet voting). However, it requires a complex mixing procedure; each stage of the mix must be performed by a different party (without mutual shared interest) for the scheme to be effective.

As we will show in Section 3, VoteBox employs homomorphic encryption [5] in order to keep track of each vote. A machine will encrypt a one for each candidate (or issue) the voter votes for and a zero elsewhere. The homomorphic property allow the encrypted votes for each candidate to be summed into a single total without being decrypted. This approach, also used by the Adder [30] and Civitas [12] Internet e-voting systems, typically combines the following elements:

Homomorphic Tallying

The encryption system allows encrypted votes to be added together by a third party without knowledge of individual vote plaintexts. Many ciphers, including El Gamal public key encryption, can be designed to have this property. Anyone can verify that the final plaintext totals are consistent with the sum of the encrypted votes.

Non-Interactive Zero Knowledge (NIZK) proofs

In any voting system, we must ensure that votes are well formed. For example, we may want to ensure that a voter has made only one selection in a race, or that the voter has not voted multiple times for the same candidate. With a plain-text ballot containing single-bit counters (i.e., 0 or 1 for each choice) this is trivial to confirm, but homomorphic counters obscure the actual counter's value with encryption. By employing NIZKs [7], a machine can include with its encrypted votes a proof that each vote is well-formed with respect to the ballot design (e.g., at most one candidate in each race received one vote, while all other candidates received zero votes). Moreover, the attached proof is zero-knowledge in the sense that the proof reveals no information that might help decrypt the encrypted vote. Note that although NIZKs like this can prevent a voting machine from grossly stuffing ballots, they cannot prevent a voting machine from flipping votes from one candidate to another.

The Bulletin Board

A common feature of most cryptographic voting systems is that all votes are posted for all the world to see. Individual voters can then verify that their votes appear on the board (e.g., locating a hash value or serial number “receipt” from their voting session within a posted list of every encrypted vote). Any individual can then recompute the homomorphic tally and verify its decryption by the election authority. Any individual could likewise verify the NIZKs.

2.4  Non-cryptographic techniques

3  Design

We now revisit our design goals from Section 1 and discuss their implementation in VoteBox, our complete prototype voting system.

3.1  User interface

Goals achieved: DRE-like user experience; minimized software stack

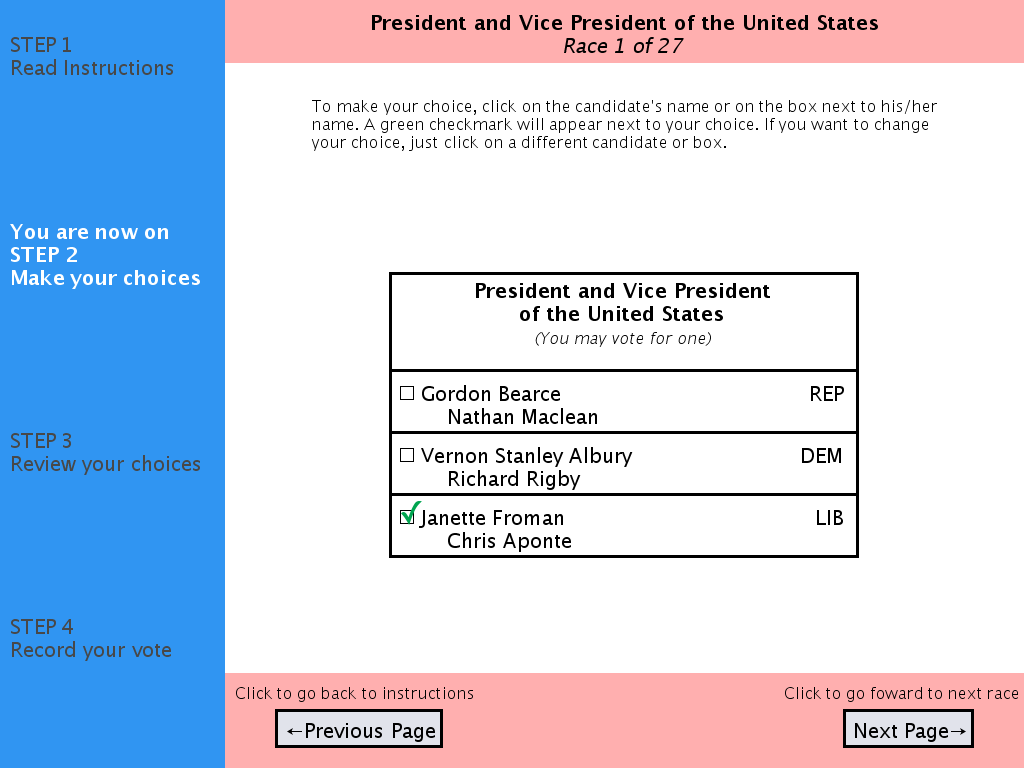
A recent study [15] bolsters much anecdotal evidence suggesting that voters strongly prefer the DRE-style electronic voting experience to more traditional methods. Cleaving to the DRE model (itself based on the archetypical computerized kiosk exemplified by bank machines, airline check-in kiosks, and the like), VoteBox presents the voter with a ballot consisting of a sequence of pages: full screens containing text and graphics. The only interactive elements of the interface are buttons: rectangular regions of the screen attached to either navigational behavior (e.g., “go to next page”) or selection behavior (“choose candidate X”). (VoteBox supports button activation via touch screen and computer mouse, as well as keyboards and assistive technologies). An example VoteBox ballot screen is shown in Figure 1.

(i)
(ii)	(iii)

Figure 1: Sample VoteBox page. The voter sees (i); a schematic for the page is shown in (ii); a subset of the pixmaps used to produce (i) are shown, along with their corresponding IDs, in (iii).

This simple interaction model lends itself naturally to the pre-rendered user interface, an idea popularized in the e-voting context by Yee's Pvote system [52, 53]. A pre-rendered ballot encapsulates both the logical content of a ballot (candidates, contests, and so forth) and the entire visual appearance down to the pixel (including all text and graphics). Generating the ballot ahead of time allows the voting machine software to perform radically fewer functions, as it is no longer required to include any code to support text rendering (including character sets, Unicode glyphs, anti-aliasing), user interface element layout (alignment, grids, sizing of elements), or any graphics rendering beyond bitmap placement.

More importantly, the entire voting machine has no need for any of these functions. The only UI-related services required by VoteBox are user input capture (in the form of (x,y) pairs for taps/clicks, or keycodes for other input devies) and the ability to draw a pixmap at a given position in the framebuffer. We therefore eliminate the need for a general-purpose GUI window system, dramatically reducing the amount of code on the voting machine.

In our pre-rendered design, the ballot consists of a set of image files, a configuration file which groups these image files into pages (and specifies the layout of each page), and a configuration file which describes the abstract content of the ballot (such as candidates, races, and propositions). This effectively reduces the voting machine's user interface runtime to a state machine which behaves as follows. Initially, the runtime displays a designated initial page (which should contain instructional information and navigational components). The voter interacts with this page by selecting one of a subset of elements on the page which have been designated in the configuration as being selectable. Such actions trigger responses in VoteBox, including transitions between pages and commitment of ballot choices, as specified by the ballot's configuration files. The generality of this approach accommodates accessibility options beyond touch-screens and visual feedback; inputs such as physical buttons and sip-and-puff devices can be used to generate selection and navigation events (including “advance to next choice”) for VoteBox. Audio feedback could also be added to VoteBox state transitions, again following the Pvote example [52].

We also built a ballot preparation tool to allow election administrators to create pre-rendered ballots for VoteBox. This tool, a graphical Java program, contains the layout and rendering logic that is omitted from VoteBox. In addition to clear benefits that come from reducing the complexity of the voting machine, this also pushes many of the things that might change from election to election or from state to state out of the voting machine. For example, Texas requires a straight-ticket voting option while California forbids it. With VoteBox, the state-specific behavior is generated by the ballot preparation tool. This greatly simplifies the software certification process, as testing labs would only need to consider a single version of VoteBox rather than separate versions customized for each state's needs. Local groups interested in the election could then examine the local ballot definitions for correctness, without needing to trust the ballot preparation tool.

3.2  Auditorium

Goals achieved: Defense against data loss; tamper-evident audit logs

The failures described in Section 2 indicate that voting machines cannot be trusted to store their own data—or, at least, must not be solely trusted with their own data. We observe that modern PC equipment is sufficiently inexpensive to be used as a platform for e-voting (and note that most DREs are in fact special-purpose enclosures and extensions on exactly this sort of general-purpose hardware). VoteBox shares with recent peer-to-peer systems research the insight that modern PCs are noticeably overprovisioned for the tasks demanded of them; this is particularly true for e-voting given the extremely minimal system requirements of the user interface described in Section 3.1. Such overpowered equipment has CPU, disk, memory, and network bandwidth to spare, and VoteBox puts these to good use addressing the problem of data loss due to election-day failure.

Figure 2: Voting in the Auditorium. VoteBoxes are connected in a broadcast network. All election events (including cast ballots) are replicated to every voting machine and entangled with hash chaining. A supervisor console allows poll workers to use the Auditorium channel to distribute instructions to voting machines (such as “you are authorized to cast a ballot”) such that those commands also enter the permanent, tamper-evident record.

Our design calls for all VoteBoxes in a polling place to be joined together in a broadcast network² as set forth in our earlier work on Auditorium [46]. An illustration of this technique can be found in Figure 2. The polling place network is not to be routable from the Internet; indeed, an air gap should exist preventing Internet packets from reaching any VoteBoxes. We will see in how data leaving the polling place is essential to our complete design; such a one-way linkage can be built while retaining an air gap [27].

Each voting machine on the network broadcasts every event it would otherwise record in its log. As a result, the loss of a single VoteBox cannot result in the loss of its votes, or even its record of other election events. As long as a single voting machine survives, there will be some record of the votes cast that day.

Supervisor console. We can treat broadcast log messages as communication packets, with the useful side effect that these communications will be logged by all participating hosts. VoteBox utilizes this feature of Auditorium to separate machine behavior into two categories: (1) features an election official would need to use, and (2) features a voter would need to use. This dichotomy directly motivates our division of VoteBox into two software artifacts: (1) the VoteBox “booth” (that is, the voting machine component that the voter interacts with, as described in Section 3.1), and (2) the “supervisor” console.

The supervisor is responsible for the coordination of all election-day events. This includes opening the polls, closing the polls, and authorizing a vote to be captured at a booth location. For more practical reasons (because the supervisor console should run on a machine in the polling place that only election officials have physical access to, and, likewise, because election officials should never need to touch any other machine in the polling place once the election is running), this console also reports the status of every other machine in the polling place (including not only connectivity status, but also various “vital sign” information, such as its battery power). During the course of an election day, poll workers are able to conduct the election entirely from the supervisor console.

In addition, as an intended design decision, the separation of election control (on the supervisor console) from voting (at the VoteBox booth) fundamentally requires that every important election event be a network communication. Because we only allow this communication to happen in the form of Auditorium broadcast messages, these communications are always logged by every participating VoteBox host (supervisors and booths included).

Hash chaining and tamper evidence. Auditorium also provides for hash chaining of log entries; when combined with broadcast replication, the result is a lattice of hash values that entangles the timelines of individual voting machines. This technique, adapted from the field of secure audit logging [33, 48], yields strong evidence of tampering or otherwise omitted or modified records. No attacker or failure can alter any individual log entry without invalidating all subsequent hashes in the record. We prevent attackers from performing this attack in advance or arrears of the election by bookending the secure log: before the polls open, a nonce (or “launch code”) is distributed, perhaps by telephone, to each polling place; this nonce is inserted into the beginning of the log. Similarly, when the polls are closed, election supervisors can quickly publish the hash of the completed log to prevent future tampering.

3.3  Cast ballots and immediate ballot challenge

Goals achieved: End-to-end verifiability

In VoteBox, cast ballots are published in the global Auditorium log, implicitly revealing the contents of the cast ballot to any party privy to the log data. This, of course, includes post-election auditors seeking to verify the validity and accuracy of the result, but it also could include partisans seeking proof of a bribed voter's choice (or some other sort of malicious activity). In fact, the contents of the cast ballot need to be encrypted (in order to preserve anonymity), but they also need to fit into a larger software independent design. That is, if the software (because of bugs or malice) corrupts a ballot before encrypting it, this corruption must be evident to the voter.

An end-to-end verifiable voting system is defined as one that can prove to the voter that (1) her vote was cast as intended and (2) her vote was counted as cast. Our design provides a challenge mechanism, which can verify the first property, along with real-time public dissemination of encrypted votes, which can satisfy the second.

Counters. We begin by encoding a cast ballot as an n-tuple of integers, each of which can be 1 or 0. Each element of the n-tuple represents a single choice a voter can make, n is the number of choices, and a value of 1 encodes a vote for the choice while 0 encodes a vote against the choice. (In the case of propositions, both “yes” and “no” each appear as a single “choice,” and in the case of candidates, each candidate is a single “choice.”) The cast ballot structure needs not be organized into races or contests; it is simply an opaque list of choice values. We define each element as an integer (rather than a bit) so that ballots can be homomorphically combined. That is, ballots A = (a₀, a₁, …) and B = (b₀, b₁, …) can be summed together to produce a third ballot S = (a₀ + b₀, a₁ + b₁, …), whose elements are the total number of votes for each choice.³

Homomorphic encryption of counters. VoteBox uses an El Gamal variant that is additively homomorphic to encrypt ballots before they are cast. Each element of the tuple is independently encrypted. The encryption and decryption functions are defined as follows:

E(c,r, ga) = 〈gr, (ga)rfc 〉 D(〈gr, garfc 〉,a) = garfc (gr)a D(〈gr, garfc 〉,r) = garfc (ga)r

where f and g are group generators, c is the plaintext counter, r is randomly generated at encryption time, a is the decryption key, and g^a is the public encryption key. To decrypt, a party needs either a or r in order to construct g^ar. (g^r, which is given as the first element of the cipher tuple, can be raised to a, or g^a, which is the public encryption key, can be raised to r.) After constructing g^ar, the decrypting party should divide the second element of the cipher tuple by this value, resulting in f^c.

To recover the counter's actual value c, we must invert the discrete logarithm f^c, which of course is difficult. As is conventional in such a situation, we accelerate this task by precomputing a reverse mapping of f^x → x for 0 < x ≤ M (for some large M) so that for expected integral values of c the search takes constant time. (We fall back to a linear search, starting at M+1, if c is not in the table.)

We now show that our encryption function is additively homomorphic by showing that when two ciphers are multiplied, their corresponding counters are added:

E(c1,r1) · E(c2,r2) = 〈gr1, gar1fc1 〉· 〈gr2, gar2fc2 〉 = 〈gr1+r2, ga(r1+r2)fc1+c2 〉

Immediate ballot challenge. To allow the voter to verify that her ballot was cast as intended, we need some way to prove to the voter that the encrypted cipher published in the Auditorium log represents the choices she actually made. This is, of course, a contentious issue wrought with negative human factors implications.

We term our solution to the first requirement of end-to-end verifiability “immediate ballot challenge,” borrowing an idea from Benaloh [4]. A voter should be able (on any arbitrary ballot) to challenge the machine to produce a proof that the ballot was cast as intended. Of course, because these challenges generally force the voting machine to reveal information that would compromise the anonymity of the voter, challenged ballots must be discarded and not counted in the election. A malicious voting system now has no knowledge of which ballots will be challenged, so it must either cast them all correctly or risk being caught if it misbehaves.

Figure 3: Challenge flow chart. As the voter advances past the review screen to the final confirmation screen, VoteBox commits to the state of the ballot by encrypting and publishing it. A challenger, having received this commitment (the encrypted ballot) out-of-band (see Figure 4), can now invoke the “challenge” function on the VoteBox, compelling it to reveal the contents of the same encrypted ballot. (A voter will instead simply choose “cast.”)

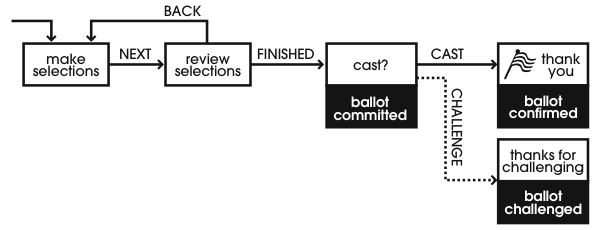
Our implementation of this idea is as follows. Before a voter has committed to her vote, in most systems, she is presented with a final confirmation page which offers two options: (1) go back and change selections, or (2) commit the vote. Our system, like Benaloh's, adds one more page at the end, giving the voter the opportunity to challenge or cast a vote. At this point, Benaloh prints a paper commitment to the vote. VoteBox will similarly encrypt and publish the cast ballot before displaying this final “challenge or cast” screen. If the voter chooses to cast her vote, VoteBox simply logs this choice and behaves as one would expect, but if the voter, instead, chooses to challenge VoteBox, it will publish the value for r that it passed to the encryption function (defined in equation 1) when it encrypted the ballot in question. Using equation 1 and this provided value of r, any party (including the voter) can decrypt and verify the contents of the ballot without knowing the decryption key. An illustration of this sequence of events is in Figure 3.

Figure 4: Voting with ballot challenges. The polling place from Figure 2 sends a copy of all log data over a one-way channel to election headquarters (not shown) which aggregates this data from many different precincts and republishes it. This enables third-party “challenge centers” to provide challenge verification services to the field.

In order to make this process immediate, we need a way for voters (or voter advocates) to safely observe Auditorium traffic and capture their own copy of the log. It is only then that the voter will be able to check, in real time, that VoteBox recorded and encrypted her preferences correctly. To do this, we propose that the local network constructed at the polling place be connected to the public Internet via a data diode [27], a physical device which will guarantee that the information flow is one way.⁴ This connectivity will allow any interested party to watch the polling location's Auditorium traffic in real time. In fact, any party could provide a web interface, suitable for access via smart phones, that could be used to see the voting challenges and perform the necessary cryptography. This arrangement is summarized in Figure 4. Additionally, on the output side of the data diode, we could provide a standard Ethernet hub, allowing challengers to locally plug in their own auditing equipment without relying on the election authority's network infrastructure. Because all Auditorium messages are digitally signed, there is no risk of the challenger being able to forge these messages.

Implications of the challenge scheme. Many states have laws against connecting voting machines or tabulation equipment to the Internet—a good idea, given the known security flaws in present equipment. Our cryptographic techniques, combined with the data diode to preserve data within the precinct, offer some mitigation against the risks of corruption in the tallying infrastructure. An observer could certainly measure the voting volume of every precinct in real-time. This is not generally considered to be private information.

VoteBox systems do not need a printer on every voting machine; however, Benaloh's printed ballot commitments offer one possibly valuable benefit: they allow any voter to take the printout home, punch the serial number into a web site, and verify the specific ballot ciphertext that belongs to them is part of the final tally, thus improving voters' confidence that their votes were counted as cast. A VoteBox lacking this printer cannot offer voters this opportunity to verify the presence of their own cast ballot ciphertexts. Challengers, of course, can verify that the ciphertexts are correctly encrypted and present in the log in real-time, thus increasing the confidence of normal voters that their votes are likewise present to be counted as cast. Optionally, Benaloh's printer mechanism could be added to VoteBox, allowing voters to take home a printed receipt specifying the ciphertext of their ballot.

Similarly, VoteBox systems do not need NIZKs. While NIZKs impose limits on the extent to which a malicious VoteBox can corrupt the election tallies by corrupting individual votes, this sort of misbehavior can be detected through our challenge mechanism. Regardless, NIZKs would integrate easily with our system and would provide an important “sanity checking” function that can apply to every ballot, rather than only the challenged ballots.

3.4  Procedures

To summarize the VoteBox design, let us review the steps involved in conducting an election with the system.

Before the election.

1. The ballot preparation software is used to create the necessary ballot definitions.
2. Ballot definitions are independently reviewed for correctness (so that the ballot preparation software need not be trusted).
3. Ballot definitions and key material (for vote encryption) are distributed to polling places along with VoteBox equipment.

Election day: opening the polls.

4. The Auditorium network is established and connected to the outside world through a data diode.
5. All supervisor consoles are powered on, connected to the Auditorium network, and one of them is enabled as the primary console (others are present for failover purposes).
6. Booth machines are powered on and connected to the Auditorium network.
7. A “launch code” is distributed to the polling place by the election administrator.
8. Poll workers open the polls by entering the launch code.

The last step results in a “polls-open” Auditorium message, which includes the launch code. All subsequent events that occur will, by virtue of hash chaining, provably have occurred after this “polls-open” message, which in turn means they will have provably occurred on or after election day.

Election day: casting votes.

9. The poll worker interacts with the supervisor console to enable a booth for the voter to use. This includes selecting a machine designated as not in use and pressing an “authorize” button.
10. The supervisor console broadcasts an authorization message directing the selected machine to interact with a voter, capture his preference, and broadcast back the result.
11. If the booth does not have a copy of the ballot definition mentioned in the authorization message, it requests that the supervisor console publish the ballot definition in a broadcast.
12. The booth graphically presents the ballot to the voter and interacts with her, capturing her choices.
13. The booth shows a review screen, listing the voter's choices.
14. If the voter needs to make changes, she can do that by navigating backward through the ballot screens. Otherwise, she indicates she is satisfied with her selections.
15. The booth publishes the encrypted ballot over the network, thereby committing to its contents. The voter may now choose one of two paths to complete her voting session:

Cast her vote by pressing a physical button. The VoteBox signals to the voter that she may exit the booth area; it also publishes a message declaring that the encrypted ballot has been officially cast and can no longer be challenged.

Challenge the machine by invoking a separate UI function. The challenged VoteBox must now reveal proof that the ballot was cast correctly. It does so by publishing the secret r used to encrypt the ballot; the ballot is no longer secret. This proof, like all Auditorium traffic, is relayed to the outside world, where a challenge verifier can validate against the earlier commitment and determine whether the machine was behaving correctly. The voter or poll workers can contact the challenge verifier out-of-band (e.g., with a smartphone's web browser) to discover the result of this challenge. Finally, the ballot committed to in step 15 is nullified by the existence of the proof in the log. The VoteBox resets its state. The challenge is complete.

Election day: closing the polls.

16. A poll worker interacts with the supervisor console, instructing it to close the polls.
17. The supervisor console broadcasts a “polls-closed” message, which is the final message that needs to go in the global log. The hash of this message is summarized on the supervisor console.
18. Poll workers note this value and promptly distribute it outside the polling place, fixing the end of the election in time (just as the beginning was fixed by the launch code).
19. Poll workers are now free to disconnect and power off VoteBoxes.

3.5  Attacks on the challenge system

Consequently, in the common case when voters wish to cast normal votes, they must not have access to the Auditorium network stream while voting. This means cellular phones and other such equipment must be banned to enforce the privacy of the voter. (Such a ban is already necessary, in practice, to defeat the use of cellular telephones to capture video evidence of a vote being cast on traditional DRE systems.)

A related attack concerns the behavior of a VoteBox once a user has gone beyond the “review selections” screen to the “cast?” screen (see Figure 3). If the voter wants to vote for Alice and the machine wants to defraud Alice, the machine could challenge votes for Alice while displaying the UI for a regular cast ballot. To address these phantom challenges, we take advantage of Auditorium. Challenge messages are broadcast to the entire network and initiate a suitable alarm on the supervisor console. For a genuine challenge, the supervisor will be expecting the alarm. Otherwise, the unexpected alarm would cue a supervisor to offer the voter a chance to vote again.⁵ As a result, a malicious VoteBox will be unable to surreptitiously challenge legitimate votes. Rather, if it misbehaved a sufficient number of times, it would be taken out of service, limiting the amount of damage it could cause.

4  Discussion

4.1  Implementation notes and experience

Development of VoteBox has been underway since May of 2006; in that time the software has gone through a number of metamorphoses that we briefly describe here.

Secure software design. When we began the VoteBox implementation project, our initial goal was to develop a research platform to explore both security and human factors aspects of the electronic voting problem. Our early security approaches were: (1) reduced trusted code base through use of PRUI due to Yee [53]; (2) software simulation of hardware-enforced separation of components after the example of Sastry et al. [47]; and (3) hardware support for strict runtime software configuration control (i.e., trusted computing hardware).

Our original strategy for achieving trustworthy hardware was to target the Xbox 360 video game platform,⁶ initially developing VoteBox as a Managed C# application. The Xbox has sophisticated hardware devoted to ensuring that the system runs only certified software programs, which is an obviously useful feature for a DRE. Additionally, video game systems are designed to be inexpensive and to withstand some abuse, making them good candidates for use in polling places. Finally, a lack of a sophisticated operating system is no problem for a prerendered user interface; we were fairly confident that an Xbox could handle displaying static pixmaps. We quickly found, however, that development for a more widely-available software platform was both easier for us and more likely to result in a usable research product.

By the end of the 2006 summer we had ported VoteBox to Java. We had no intention of relying on Java's AWT graphical interface (and its dependency, in turn, on a window system such as X or Windows). Instead, we intended to develop VoteBox atop SDL, the Simple DirectMedia Layer,⁷ a dramatically simpler graphics stack. (The Pvote system also uses SDL as a side-effect of its dependency on the Pygame library [52].) Regrettably, the available Java bindings for SDL suffered from stability problems, forcing us to run our PRUI atop a limited subset of AWT (including only blitting and user input events).

Our intended approach to hardware-inspired software module separation was twofold: force all modules to interact with one another through observable software “wires,” and re-start the Java VM between voters to prevent any objects lingering from one voting session to the next. Both of these ideas are due to Sastry's example. In the end, only the latter survived in our design; VoteBox essentially “reboots” between voters, but complexity and time constraints made our early software wire prototypes unworkable.

Insecure software design. As mentioned above, we intended from the beginning that VoteBox would serve as a foundation for e-voting research of different stripes, including human factors studies. This would prove to be its earliest test; VoteBox found use in various studies carried out by Byrne, Everett, and Greene between 2006 and 2008 [15, 16]. Working in close coordination with these researchers, we developed ballot designs and tuned the VoteBox user experience to meet their research needs. (The specific graphic design of the ballot shown in Figure 1 is owed to this collaboration.)

We also modified VoteBox to emit fine-grained data tracking the user's every move: the order of visited screens, the time taken to make choices, and so forth. This sort of functionality would be considered a breach of voter privacy in a real voting system, so we took great pains to make very clear the portions of the code that were inserted for human factors studies. Essential portions of this code were sequestered in a separate module that could be left out of compilation to ensure that no data collection can happen on a “real” VoteBox; later we made this distinction even more stark by dividing the VoteBox codebase into two branches in our source control system.

It is noteworthy that some of the most interesting human factors results [16,studies 2 and 3] require a malicious VoteBox. One study measured how likely voters are to notice if contests are omitted from the review screen; another, if votes on the review screen are flipped from the voter's actual selection. If data collection functionality accidentally left in a “real” VoteBox is bad, this code is far worse. We added the word “evil” to the names of the relevant classes and methods so that there would be no confusion in a code auditing scenario.

S-expressions. When it came time to develop the Auditorium network protocol, we chose to use a subset of the S-expression syntax defined by Rivest [38]. Previous experiences with peer-to-peer systems that used the convenient Java ObjectOutputStream for data serialization resulted in protocols that were awkwardly bound to particular implementation details of the code, were difficult to debug by observation of data on the wire, and were inexorably bound to Java.

S-expressions, in particular the canonical representation used in Auditorium, are a general-purpose, portable data representation designed for maximum readability while at the same time being completely unambiguous. They are therefore convenient for debugging while still being suitable for data that must be hashed or signed. By contrast, XML requires a myriad of canonicalization algorithms when used with digital signatures; we were happy to leave this large suite of functionality out of VoteBox.

We quickly found S-exps to be convenient for other portions of VoteBox. They form the disk format for our secure logs (as carbon-copies of network traffic, this is unsurprising). Pattern matching and match capture, which we added to our S-exp library initially to facilitate parsing of Auditorium messages, subsequently found heavy use at the core of Querifier [44], our secure log constraints checker, allowing its rule syntax to be naturally expressed as S-exps. Even the human factors branch of VoteBox dumps user behavior data in S-expressions.

Code size.   Table 1 lists several code size metrics for the modules in VoteBox, including all unit tests. We aspired to the compactness of Pvote's 460 Python source lines [52], but the expanded functionality of our system, combined with the verbosity of Java (especially when written in clear, modern object-oriented style) resulted in a much larger code base. The votebox module (analogous to Pvote's functionality) contains nearly twenty times as many lines of code. The complete VoteBox codebase, however, compares quite favorably with current DRE systems, making thorough inspection of the source code a tractable proposition.

4.2  Performance evaluation and estimates

By building a prototype implementation of our design, we are able to validate that it operates within reasonable time and space bounds. Some aspects of VoteBox require “real time” operation while others can safely take minutes or hours to complete.

Log publication. Recall that VoteBoxes, by virtue of the fact that they communicate with one another using the Auditorium protocol, produce s-expression log data which serves as a representation of the events that happened during the election. An important design goal is the allowance of outside parties to see this log data in real time; our immediate ballot challenge protocol relies on it.

We've assumed, as a worst case, that the polling place is connected to election central with a traditional modem. This practical bandwidth limitation forces us to explore the size of the relevant log messages and examine their impact on the time it takes to perform an immediate ballot challenge. This problem is only relevant if the verification machine is not placed on the polling place network (on the public side of the data diode). With the verification machine on the LAN, standard network technology will be able to transmit the log data much faster than any reasonable polling place could generate it.

A single voter's interaction with the polling place results in in the following messages: (1) an authorization message from the supervisor to the booth shortly after the voter enters the polling place, (2) a commitment message broadcast by the booth after the voter is done voting, (3) either a cast ballot message or a challenge response message (the former if the voter decides to cast and the latter if the voter decides to challenge), (4) and an acknowledgment from the supervisor that the cast ballot or challenge has been received, which effectively allows the machine to release its state and wait for the next authorization.

Assuming all the crypto keys are 1024-bits long, an authorization-to-cast message is 1 KB. Assuming 30 selectable elements are on the ballot, both commit and cast messages are 13 KB while challenge response messages are 7 KB. An acknowledgment is 1 KB.

We expect a good modem's throughput to be 5 KB/second. The challenger must ask the machine to commit to a vote, wait for the verification host to receive the commitment, then ask the machine to challenge the vote. (The voter must wait for proof of the booth's commitment in order for the protocol to work.) In the best case, when only one voter is in the polling place (and the uploader's buffer is empty), a commitment can be immediately transmitted. This takes under 3 seconds. The challenge response can be transmitted in under 2 seconds. In the worst case, when as many as 19 other voters have asked their respective booths to commit and cast their ballots, the challenger must wait for approximately 494 KB of data to be uploaded (on behalf of the other voters). This would take approximately 100 seconds. Assuming 19 additional voters, in this short time, were given access to booths and all completed their ballots, the challenger might be forced to wait another 100 seconds before the challenge response (the list of r-values used to encrypt the first commitment) could make it through the queue.

Therefore, in the absolute worst case situation (30 elements on the ballot and 20 machines in the polling place), the challenger is delayed by a maximum of 200 seconds due to bandwidth limitations.

Encryption. Because a commitment is an encrypted version of the cast ballot, a cast ballot must be encrypted before a commitment to it is published. Furthermore, the verifier must do a decryption in order to verify the result of a challenge. Encryption and decryption are always a potential source of delay, therefore we examine our implementation's encryption performance here.

Recall that a cast ballot is an n-tuple of integers, and an encrypted cast ballot has each of these integers encrypted using our additively homomorphic El Gamal encryption function. We benchmarked the encryption of a reference 30 candidate ballot; on a Pentium M 1.8 GHz laptop it took 10.29 CPU seconds, and on an Opteron 2.6 GHz server it took 2.34 CPU seconds. We also benchmarked the decryption, using the r-values generated by the encryption function (simulating the work of a verification machine in the immediate ballot challenge protocol). On the laptop, this decryption took 5.18 CPU seconds, and on the server it took 1.27 CPU seconds.

The runtime of this encryption and decryption will be roughly the same. However, there is one caveat. To make our encryption function additively homomorphic, we exponentiate a group member (called f in equation 1) by the plaintext counter (called c in equation 1). (The result is that when this value is multiplied, the original counter gets added “in the exponent.”) Because discrete log is a hard problem, this exponentiation cannot be reversed. Instead, our implementation stores a precomputed table of encryptions of low counter values. We assumes that, in real elections, these counters will never be above some reasonable threshold (we chose 20,000). Supporting counters larger than our precomputed table would require a very expensive search for the proper value.

This is never an issue in practice, since individual ballots only ever encrypt the values 0 and 1, and there will never be more than a few thousand votes per day in a given precinct. While there may be a substantially larger number of votes across a large city, the election official only needs to perform the homomorphic addition and decryption on a precinct-by-precinct basis.⁸ This also allows election officials to derive per-precinct subtotals, which are customarily reported today and are not considered to violate voter privacy. Final election-night tallies are computed by adding the plaintext sums from each precinct.

Log analysis. There are many properties of the published logs that we might wish to validate, such as ensuring that all votes were cast while the polls were open, that no vote is cast without a prior authorization sharing the same nonce, and so on. These properties can be validated by hand, but are also amenable to automatic analysis. We built a tool called Querifier [44, 45] that performs this function based on logical predicates expressed over the logs. None of these queries need to be validated in real time, so performance is less critical, so long as answers are available within hours or even days after the election.

4.3  Security discussion

Beyond the security goals introduced in Section 1 and elaborated in Section 3, we offer a few further explorations of the security properties of our design.

Ballot decryption key material. We have thus far avoided the topic of which parties are entitled to decrypt the finished tally, assuming that there exists a single entity (perhaps the director of elections) holding an El Gamal private key. We can instead break the decryption key up into shares [49, 13] and distribute them to several mutually-untrusting individuals, such as representatives of each major political party, forcing them to cooperate to view the final totals.

This may be insufficient to accommodate varying legal requirements. Some jurisdictions require that each county, or even each polling place, be able to generate its own tallies on the spot once the polls close. In this case we must create separate key material for each tallying party, complicating the matter of who should hold the decryption key. Our design frees us to place the decryption key on, e.g., the supervisor console, or a USB key held by a local election administrator. We can also use threshold decryption to distribute key shares among multiple VoteBoxes in the polling place or among mutually-untrusting individuals present in the polling place.

Randomness. Our El Gamal-based cryptosystem, like many others, relies on the generation of random numbers as part of the encryption process. Since the ciphertext includes g^r, a malicious voting machine could perform O(2^k) computations to encode k bits in g^r, perhaps leaking information about voters' selections. Karlof et al. [28] suggest several possible solutions, including the use of trusted hardware. Verifiable randomness may also be possible as a network service or a multi-party computation within the VoteBox network [21].

Mega attacks. We believe the Auditorium network offers defense against mishaps and failures of the sort already known to have occurred in real elections. We further expect the networked architecture to provide some defense against more extreme failures and attacks that are hypothetical in nature but nonetheless quite serious. These “mega attacks,” such as post-facto switched results, election-day shadow polling places, and armed booth capture (described more fully in previous work [46]), are challenges for any electronic voting system (and even most older voting technologies as well).

5  Conclusions and future work

In this paper we have shown how the VoteBox system design is a response to threats, real and hypothesized, against the trustworthiness of electronic voting. Recognizing that voters prefer a DRE-style system, we endeavored to create a software platform for e-voting projects and then assembled a complete system using techniques and ideas from current research in the field. VoteBox creates audit logs that are believable in the event of a post-facto audit, and it does this using the Auditorium networking layer, allowing for convenient administration of polls as well as redundancy in case of failure. Its code complexity is kept under control by moving inessential graphics code outside the trusted system, with the side effect that ballot descriptions can be created—and audited—long before election day. Finally, the immediate ballot capture technique gives real power to random machine audits. Any voter can ask to challenge any voting machine, and the machine has no way to know it is under test before it commits to the contents of the encrypted ballot.

VoteBox is a complete system and yet still an ongoing effort. It is still being actively used for human factors experimentation, work which spurs evolution and maturity of the software. Many of VoteBox's features were designed with human factors of both poll workers and voters in mind. Evaluating these with human subject testing would make a fascinating study. For example, we could evaluate the rate at which voters accidentally challenge ballots, or we could ask voters to become challengers and see if they can correctly catch a faulty machine.

We have a number of additional features and improvements we intend to add or are in the process of adding to the system as well. Because one of the chief benefits of the DRE is its accessibility potential, we anticipate adding support for unusual input devices; similarly, following the example of Pvote, we expect that VoteBox's ballot state machines will map naturally onto the problem of providing a complete audio feedback experience to match the video display. As we continue to support human factors testing, it is obviously of interest to continue to maintain a clear separation and identification of “evil” code; techniques to statically determine whether this code (or other malicious code) is present in VoteBox will increase our assurance in the system. We are in the process of integrating NIZK proofs into our El Gamal encrypted vote counters, further bolstering out assurance that VoteBox systems are behaving correctly. We intend to expand our use of Querifier to automatically and conveniently analyze Auditorium logs and confirm that they represent valid election events. A tabulation system for VoteBox is another logical addition to the architecture, completing the entire election life cycle from ballot design through election-day voting (and testing) to post-election auditing and vote tabulation. Finally, we note that as a successful story of combining complementary e-voting research advances, we are on the lookout for other suitable techniques to include in the infrastructure to further enhance the end-to-end verifiability, in hope of approaching true software independence in a voter-acceptable way.

Acknowledgments

This work was funded in part by NSF grants CNS-0524211 and CNS-0509297. Portions of this work took place during Wallach's sabbatical at Stanford and SRI and during Derr's internship at SRI; we thank those institutions for their support. We also thank Ben Adida, Josh Benaloh, Peter Neumann, Chris Piekert, and Brent Waters for many helpful discussions on the VoteBox architecture. In addition to the authors of this paper, the following Rice students have contributed to the VoteBox codebase: Emily Fortuna, George Mastrogiannis, Kevin Montrose, Corey Shaw, and Ted Torous. We also acknowledge Mike Byrne, Sarah Everett, and Kristen Greene for designing VoteBox's ballots. Finally, we thank the anonymous referees for their helpful and detailed feedback.

Notes

References

[1]

Final Report of the Cuyahoga Election Review Panel, July 2006. http://cuyahogavoting.org/CERP_Final_Report_20060720.pdf.

[2]

A. Ash and J. Lamperti. Florida 2006: Can statistics tell us who won Congressional District-13? Chance, 21(2), Spring 2008.

[3]

N. Barkakati. Results of GAO's Testing of Voting Systems Used in Sarasota County in Florida's 13th Congressional District. Government Accountability Office, Feb. 2008. Report number GAO-08-425T.

[4]

J. Benaloh. Ballot casting assurance via voter-initiated poll station auditing. In Proceedings of the 2nd USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Boston, MA, Aug. 2007.

[5]

J. D. C. Benaloh. Verifiable Secret-Ballot Elections. PhD thesis, Yale University Department of Computer Science, 1987.

[6]

M. Blaze, A. Cordero, S. Engle, C. Karlof, N. Sastry, M. Sherr, T. Stegers, and K.-P. Yee. Source Code Review of the Sequoia Voting System. California Secretary of State's “Top to Bottom” Review, July 2007. http://www.sos.ca.gov/elections/voting_systems/ttbr/sequoia-source-public-jul26.pdf.

[7]

M. Blum, P. Feldman, and S. Micali. Non-interactive zero-knowledge and its applications. In STOC '88: Proceedings of the twentieth annual ACM symposium on Theory of computing, pages 103-112, New York, NY, USA, 1988.

[8]

J. A. Calandrino, A. J. Feldman, J. A. Halderman, D. Wagner, H. Yu, and W. P. Zeller. Source Code Review of the Diebold Voting System. California Secretary of State's “Top to Bottom” Review, July 2007. http://www.sos.ca.gov/elections/voting_systems/ttbr/diebold-source-public-jul29.pdf.

[9]

D. Chaum. Untraceable electronic mail, return addresses, and digital pseudonyms. Communications of the ACM, 24(2), Feb. 1981.

[10]

D. Chaum, P. Y. A. Ryan, and S. A. Schneider. A practical, voter-verifiable election scheme. In ESORICS '05, pages 118-139, Milan, Italy, 2005.

[11]

M. Cherney. Vote results further delayed. The Sun News, Jan. 2008. http://www.myrtlebeachonline.com/news/local/story/321972.html.

[12]

M. R. Clarkson, S. Chong, and A. C. Myers. Civitas: A secure voting system. In IEEE Symposium on Security and Privacy, Oakland, CA, May 2008.

[13]

Y. Desmedt and Y. Frankel. Threshold cryptosystems. In CRYPTO '89: Proceedings of the 9th Annual International Cryptology Conference on Advances in Cryptology, pages 307-315, Santa Barbara, CA, July 1989.

[14]

D. L. Dill and D. S. Wallach. Stones Unturned: Gaps in the Investigation of Sarasota's Disputed Congressional Election, Apr. 2007. http://www.cs.rice.edu/~dwallach/pub/sarasota07.html.

[15]

S. Everett, K. Greene, M. Byrne, D. Wallach, K. Derr, D. Sandler, and T. Torous. Is newer always better? The usability of electronic voting machines versus traditional methods. In Proceedings of CHI 2008, Florence, Italy, Apr. 2008.

[16]

S. P. Everett. The Usability of Electronic Voting Machines and How Votes Can Be Changed Without Detection. PhD thesis, Rice University, Houston, TX, 2007.

[17]

K. Fisher, R. Carback, and T. Sherman. Punchscan: Introduction and system definition of a high-integrity election system. In Workshop On Trustworthy Elections (WOTE 2006), Cambridge, U.K., June 2006.

[18]

Florida Department of State, Division of Elections, Tallahassee, Florida. Parallel Test Summary Report, Dec. 2006. http://election.dos.state.fl.us/pdf/parallelTestSumReprt12-18-06.pdf.

[19]

Florida Department of State, Division of Elections, Tallahassee, Florida. Audit Report of the Election Systems and Software, Inc's, iVotronic Voting System in the 2006 General Election for Sarasota County, Florida, Feb. 2007. http://election.dos.state.fl.us/pdf/auditReportSarasota.pdf.

[20]

L. Frisina, M. C. Herron, J. Honaker, and J. B. Lewis. Ballot Formats, Touchscreens, and Undervotes: A Study of the 2006 Midterm Elections in Florida. Dartmouth College and The University of California at Los Angeles, May 2007. Originally released Nov. 2006, current draft available at http://www.dartmouth.edu/~herron/cd13.pdf.

[21]

R. Gardner, S. Garera, and A. D. Rubin. Protecting against privacy compromise and ballot stuffing by eliminating non-determinism from end-to-end voting schemes. Technical Report 245631, Johns Hopkins University, Apr. 2008. http://www.cs.jhu.edu/~ryan/voting_randomness/ggr_voting_randomness.pdf.

[22]

S. N. Goggin and M. D. Byrne. An examination of the auditability of voter verified paper audit trail (VVPAT) ballots. In Proceedings of the 2nd USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Berkeley, CA, USA, Aug. 2007.

[23]

S. Hertzberg. DRE Analysis for May 2006 Primary, Cuyahoga County, Ohio. Election Science Institute, San Francisco, CA, Aug. 2006. http://bocc.cuyahogacounty.us/GSC/pdf/esi_cuyahoga_final.pdf.

[24]

S. Inguva, E. Rescorla, H. Shacham, and D. S. Wallach. Source Code Review of the Hart InterCivic Voting System. California Secretary of State's “Top to Bottom” Review, July 2007. http://www.sos.ca.gov/elections/voting_systems/ttbr/Hart-source-public.pdf.

[25]

D. Jefferson. What happened in Sarasota County? The Bridge (National Academy of Engineering), 37(2), Summer 2007. Also available online at http://www.nae.edu/nae/bridgecom.nsf/weblinks/MKEZ-744KWK?OpenDocument.

[26]

D. W. Jones. Parallel testing during an election, 2004. http://www.cs.uiowa.edu/~jones/voting/testing.shtml#parallel.

[27]

D. W. Jones and T. C. Bowersox. Secure data export and auditing using data diodes. In Proceedings of the USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Vancouver, B.C., Canada, Aug. 2006.

[28]

C. Karlof, N. Sastry, and D. Wagner. Cryptographic voting protocols: A systems perspective. In USENIX Security Symposium, Aug. 2005.

[29]

J. Kelsey, A. Regenscheid, T. Moran, and D. Chaum. Hacking paper: Some random attacks on paper-based E2E systems. Presentation in Seminar 07311: Frontiers of Electronic Voting, 29.07.07-03.08.07, organized in The International Conference and Research Center for Computer Science (IBFI, Schloss Dagstuhl, Germany), Aug. 2007. http://kathrin.dagstuhl.de/files/Materials/07/07311/07311.KelseyJohn.Slides.pdf.

[30]

A. Kiayias, M. Korman, and D. Walluck. An Internet voting system supporting user privacy. In ACSAC '06: Proceedings of the 22nd Annual Computer Security Applications Conference, pages 165-174, Washington, DC, USA, 2006.

[31]

A. Kiayias and M. Yung. The vector-ballot e-voting approach. In FC'04: Financial Cryptography 2004, Key West, FL, Feb. 2004.

[32]

T. Kohno, A. Stubblefield, A. D. Rubin, and D. S. Wallach. Analysis of an electronic voting system. In Proc. of IEEE Symposium on Security & Privacy, Oakland, CA, 2004.

[33]

P. Maniatis and M. Baker. Secure history preservation through timeline entanglement. In Proceedings of the 11th USENIX Security Symposium, San Francisco, CA, Aug. 2002.

[34]

W. R. Mebane and D. L. Dill. Factors Associated with the Excessive CD-13 Undervote in the 2006 General Election in Sarasota County, Florida. Cornell University and Stanford University, Jan. 2007. http://macht.arts.cornell.edu/wrm1/smachines1.pdf.

[35]

C. A. Neff. A verifiable secret shuffle and its application to e-voting. In CCS '01: Proceedings of the 8th ACM Conference on Computer and Communications Security, pages 116-125, Philadelphia, PA, 2001.

[36]

S. Pynchon and K. Garber. Sarasota's Vanished Votes: An Investigation into the Cause of Uncounted Votes in the 2006 Congressional District 13 Race in Sarasota County, Florida. Florida Fair Elections Center, DeLand, Florida, Jan. 2008. http://www.floridafairelections.org/reports/Vanishing_Votes.pdf.

[37]

D. Rather. The trouble with touch screens. Broadcast on HDNet, also available at http://www.hd.net/drr227.html, Aug. 2007.

[38]

R. L. Rivest. S-expressions. IETF Internet Draft, May 1997. http://people.csail.mit.edu/rivest/sexp.txt.

[39]

R. L. Rivest. The ThreeBallot voting system. http://theory.csail.mit.edu/~rivest/Rivest-TheThreeBallotVotingSystem.pdf, Oct. 2006.

[40]

R. L. Rivest and W. D. Smith. Three voting protocols: ThreeBallot, VAV, and Twin. In Proceedings of the 2nd USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Boston, MA, Aug. 2007.

[41]

R. L. Rivest and J. P. Wack. On the notion of “software independence” in voting systems, 2006. http://vote.nist.gov/SI-in-voting.pdf.

[42]

P. Y. A. Ryan and T. Peacock. A threat analysis of Prêt à Voter. In Workshop On Trustworthy Elections (WOTE 2006), Cambridge, U.K., June 2006.

[43]

K. Sako and J. Kilian. Receipt-free mix-type voting scheme - a pracitcal solution to the implementation of a voting booth. In Advances in Cryptology: EUROCRYPT '95, volume 921 of Lecture Notes in Computer Science, pages 393-403. Springer-Verlag, 1995.

[44]

D. Sandler, K. Derr, S. Crosby, and D. S. Wallach. Finding the evidence in tamper-evident logs. Technical Report TR08-01, Department of Computer Science, Rice University, Houston, TX, Jan. 2008. http://cohesion.rice.edu/engineering/computerscience/TR/TR_Download.cfm?SDID=238.

[45]

D. Sandler, K. Derr, S. Crosby, and D. S. Wallach. Finding the evidence in tamper-evident logs. In Proceedings of the 3rd International Workshop on Systematic Approaches to Digital Forensic Engineering (SADFE'08), Oakland, CA, May 2008.

[46]

D. Sandler and D. S. Wallach. Casting votes in the Auditorium. In Proceedings of the 2nd USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Boston, MA, Aug. 2007.

[47]

N. Sastry, T. Kohno, and D. Wagner. Designing voting machines for verification. In Proceedings of the 15th USENIX Security Symposium, Vancouver, B.C., Canada, Aug. 2006.

[48]

B. Schneier and J. Kelsey. Secure audit logs to support computer forensics. ACM Transactions on Information and System Security, 1(3), 1999.

[49]

A. Shamir. How to share a secret. Communications of the ACM, 22(11):612-613, 1979.

[50]

C. Stewart, III. Plaintiff Jennings Ex. 8. (for Dec. 19, 2006 evidentiary hr'g), Jennings v. Elections Canvassing Comm'n of the State of Florida et al., No. 2006 CA 2973 (Circuit Ct. of the 2d Judicial Circuit, Leon County, Fla., filed Nov. 20, 2006), reproduced in 2 Appendix to Emergency Petition for a Writ of Certiorari A-579-80, Jennings v. Elections Canvassing Comm'n of the State of Florida et al., No. 1D07-11 (Fla. 1st Dist. Ct. of Appeal, filed Jan. 3, 2007), Dec. 2006.

[51]

A. Yasinsac, D. Wagner, M. Bishop, T. Baker, B. de Medeiros, G. Tyson, M. Shamos, and M. Burmester. Software Review and Security Analysis of the ES&S iVotronic 8.0.1.2 Voting Machine Firmware. Security and Assurance in Information Technology Laboratory, Florida State University, Tallahassee, Florida, Feb. 2007. http://election.dos.state.fl.us/pdf/FinalAudRepSAIT.pdf.

[52]

K.-P. Yee. Extending prerendered-interface voting software to support accessibility and other ballot features. In Proceedings of the 2nd USENIX/ACCURATE Electronic Voting Technology Workshop (EVT'07), Boston, MA, Aug. 2007.

[53]

K.-P. Yee, D. Wagner, M. Hearst, and S. M. Bellovin. Prerendered user interfaces for higher-assurance electronic voting. In USENIX/ACCURATE Electronic Voting Technology Workshop, Vancouver, B.C., Canada, 2006.